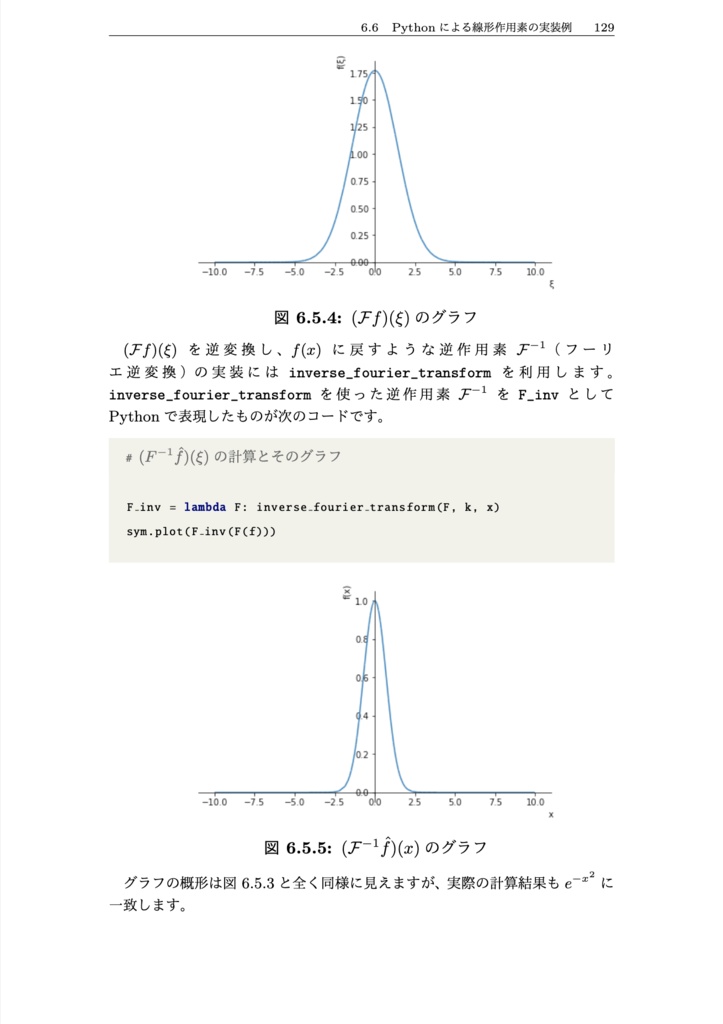
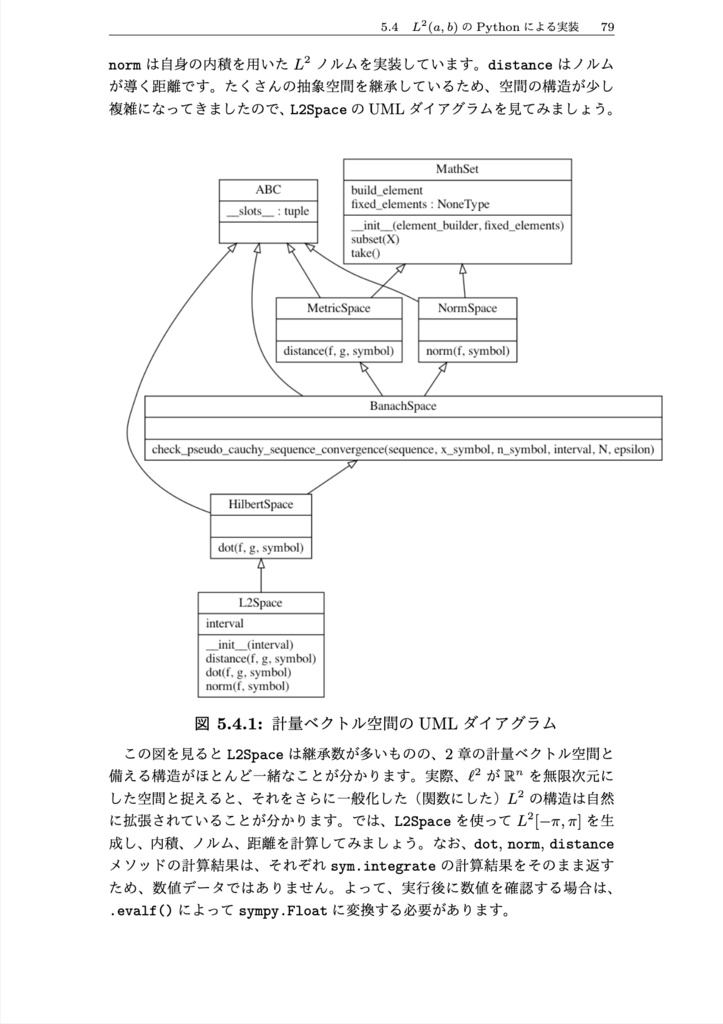
Pythonコードを交えて学ぶ関数解析
- ダウンロード商品¥ 500
■本書の内容 本書は関数解析の入門書ですが、関数解析はとても抽象的な理論を多く扱います。よって、プログラミングで表現可能な理論に関してはPythonを用いてその理論を再現し、抽象的な概念をある程度コードで追えるようなことをひとつの目標としています。扱う分野に関しては、目次を御覧ください。また、noteで第2章までの試し読みを公開しておりますので、本書に興味を持っていただいた方は先に試し読みを読まれることをおすすめします。 試し読みはこちら: https://note.com/noppoman/n/n7f208564351d ページ数: 189P + まえがき、あとがき等 ■サポートページ ソースコードや正誤表については以下のサポートページへアクセスください。 https://github.com/noppoMan/learning-functional-analysis-with-python ■ 本書を購入して読み進める前に Pythonを交えて学ぶ~というタイトルの通り、本書はある程度数学の素養があるプログラミング経験者に向けた関数解析の入門書となっています。特に書籍内では詳しく言及しませんが、前提知識として必要となる分野に ・集合と写像(集合の概念や集合の記号については1章で概説します) ・線形代数全般(ベクトル空間の基本的な性質は2章で復習します) ・解析学の基礎および微分積分の基本 ・Pythonの基本や本書で扱うライブラリ(numpyやsympy、matplotlibなど)の使い方 があります。 各章における定義や定理の証明は一般的な工学書に比べるとより厳密で抽象度が高いものになっていますので、その理解を補助するものとしてPythonコードを付属させるという構成となっています。しなしながら、関数解析はよく無限次元の線形代数といわれますが、その名の通り、無限次元で理論を展開する性質上、どうしてもコード化が難しい点もあるので、すべての理論についてもれなくコードが付属することではないことを予めご留意ください。どのようなコードが付属するかについては、サポートページをご参照ください。(本書を購入していなくてもコードについては閲覧可能です。 ■目次 第1章 集合と論理の復習 1.1 集合の記号 1.2 論理の記号 1.2.1 論理式による集合の構成 1.3 Pythonによる集合の実装 1.3.1 数学とコンピュータにおける集合の取り扱いの違い 1.3.2 基礎集合クラスの実装 第2章 ベクトル空間 2.1 ベクトル空間(線形空間) 2.2 計量ベクトル空間 2.3 計量ベクトル空間Rn のPythonによる実装 2.3.1 計量ベクトル空間 第3章 ノルム空間 3.1 ノルム空間 3.2 距離 3.3 収束と極限 3.4 バナッハ空間 3.4.1 実数の完備性 3.4.2 ノルム空間の完備性 3.5 バナッハ空間C[a,b]のPythonによる実装 第4章 ルベーグ積分 - クイックガイド 4.1 リーマン積分の課題とルベーグ積分の導入 4.1.1 リーマン積分からルベーグ積分へ 4.2 本書で必要なルベーグ積分に関する定義・定理 第5章 ヒルベルト空間 5.1 l2空間 5.2 ヒルベルト空間の定義 5.3 関数空間L2(a,b) 5.4 L2(a,b)のPythonによる実装 5.5直交補空間と直和分解 5.5.1直交補空間のPythonによる実装 5.6 正規直交系 5.7 フーリエ展開 5.8 フーリエ展開のPythonによる実装 5.9 ヒルベルト空間とl2の対応 第6章 線形作用素 6.1 線形作用素 6.2有界線形作用素 コーヒーブレイク - 主成分分析と行列の作用素ノルム 6.3 有界線形作用素のつくる空間 6.3.1 恒等作用素 6.4 逆作用素 6.5 Pythonによる線形作用素の実装例 6.6 線形汎関数 6.6.1 第二共役空間 第7章 超関数 7.1 弱収束 7.1.1 ディラックのデルタ関数 7.2 超関数 7.2.1 超関数 7.2.2 超関数の空間 7.2.3 L1上のフーリエ変換 7.2.4 急減少関数とフーリエ変換 7.2.5 Python によるフーリエ変換の理論の確認 7.2.6 超関数のフーリエ変換 7.2.7 超関数の多変数への拡張